Hello my fellow Padawans
Couple days ago I had to use an algorithm for comparing string and I want to write something about Levenshtein Algorithm. This algorithm is for measure the metric distance between 2 string text. Informally, the Levenshtein distance between two words is the minimum number of single-character edits (insertions, deletions or substitutions) required to change one word into the other. It is named after the Soviet mathematician Vladimir Levenshtein, who considered this distance in 1965.
Mathematically, the Levenshtein distance between two strings a, b (of length |a| and |b| respectively) is given by leva,b(|a|,|b|)

where 1(ai≠bi) is the indicator function equal to 0 when ai≠bi and equal to 1 otherwise, and leva, b(i,j) is the distance between the first i characters of a and the first j characters of b.
Note that the first element in the minimum corresponds to deletion (from a to b), the second to insertion and the third to match or mismatch, depending on whether the respective symbols are the same.
We can use this algorithm for string matching and spell checking
This algorithm calculates the number of edit operation that are necessary to modify one string to another string. Fro using this algorithm for dynamic programming we can use these steps :
1- A matrix is initialized measuring in the (m, n) cells the Levenshtein distance between the m-character prefix of one with the n-prefix of the other word.
2 – The matrix can be filled from the upper left to the lower right corner.
3- Each jump horizontally or vertically corresponds to an insert or a delete, respectively.
4- The cost is normally set to 1 for each of the operations.
5- The diagonal jump can cost either one, if the two characters in the row and column do not match else 0, if they match. Each cell always minimizes the cost locally.
6- This way the number in the lower right corner is the Levenshtein distance between these words.
An example that features the comparison of “HONDA” and “HYUNDAI”,
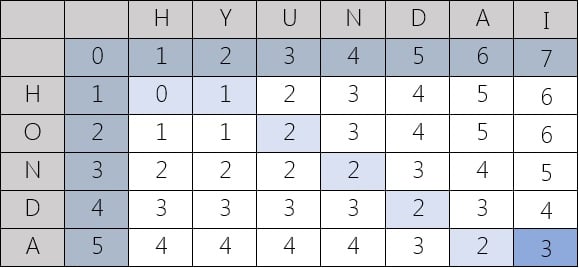
Following are two representations: Levenshtein distance between “HONDA” and “HYUNDAI” is 3.
The Levenshtein distance can also be computed between two longer strings. But the cost to compute it, which is roughly proportional to the product of the two string lengths, makes this impractical. Thus, when used to aid in fuzzy string searching in applications such as record linkage, the compared strings are usually short to help improve speed of comparisons.
Here’s the code that you can use the Levenshtein Distance and calculate percentage between 2 string.
See the Pen levenshtein.js by mzekiosmancik (@mzekiosmancik) on CodePen.

