Have you ever considered the process by which computers store floating-point numbers such as 3.1416 (𝝿) or 9.109 × 10⁻³¹ (the mass of the electron in kg) in the memory which is limited by a finite number of ones and zeroes (aka bits)?
For integers (i.e., 17). It appears to be fairly straightforward. Assume we have 16 bits (2 bytes) to store the number. We can store integers between 0 and 65535 in 16 bits:
(0000000000000000)₂ = (0)₁₀
(0000000000010001)₂ =
(1 × 2⁴) +
(0 × 2³) +
(0 × 2²) +
(0 × 2¹) +
(1 × 2⁰) = (17)₁₀
(1111111111111111)₂ =
(1 × 2¹⁵) +
(1 × 2¹⁴) +
(1 × 2¹³) +
(1 × 2¹²) +
(1 × 2¹¹) +
(1 × 2¹⁰) +
(1 × 2⁹) +
(1 × 2⁸) +
(1 × 2⁷) +
(1 × 2⁶) +
(1 × 2⁵) +
(1 × 2⁴) +
(1 × 2³) +
(1 × 2²) +
(1 × 2¹) +
(1 × 2⁰) = (65535)₁₀On the off chance that we really want a marked number we might utilize two’s supplement and shift the scope of [0, 65535] towards the negative numbers. For this situation, our 16 pieces would address the numbers in a scope of [-32768, +32767].
As you would have seen, this approach will not permit you to address the numbers like – 27.15625 (numbers after the decimal point are simply being disregarded).
However, we’re not the initial ones who have seen this issue. Around ≈36 years ago a few brilliant people conquered this limit by presenting the IEEE 754 norm for floating-point arithmetic.
The IEEE 754 standard portrays the way (the framework) of utilizing those 16 bits (or 32, or 64 bits) to store the numbers of wider range, including the small floating numbers (smaller than 1 and closer to 0).
To get the thought behind the standard we could review the logical documentation – an approach to communicating numbers that are excessively huge or excessively little (for the most part would bring about a long string of digits) to be helpfully written in decimal structure.
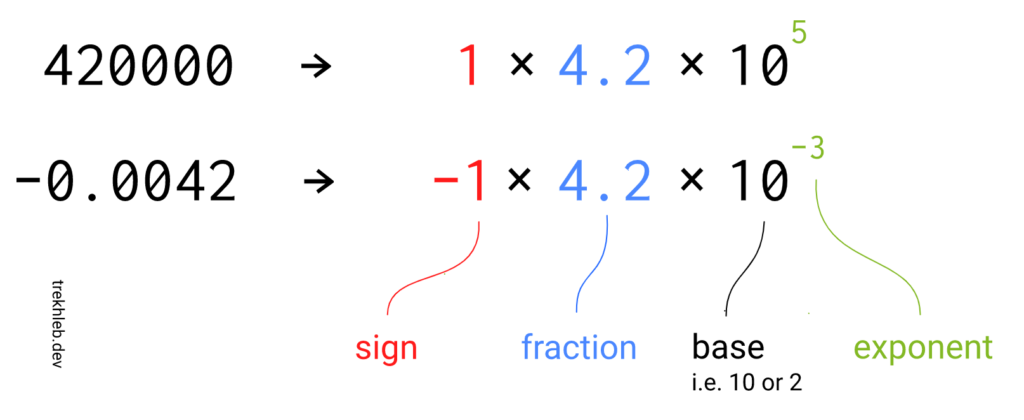
As you might see from the picture, the number portrayal may be parted into three sections:
sign
division (otherwise known as significant) – the important digits (the significance, the payload) of the number
example – controls how far and in which direction to move the decimal point in the fraction
The base part we might preclude simply by settling on what it will be equivalent to. For our situation, we’ll involve 2 as a base.
Rather than utilizing every one of the 16 bits (or 32 bits, or 64 bits) to store the fraction of the number, we might share the bits and store a sign, type, and portion simultaneously. Contingent upon the numbers of bits that we will use to store the number we end up with the accompanying parts:
| Floating-point format | Total bits | Sign bits | Exponent bits | Fraction bits | Base |
|---|---|---|---|---|---|
| Half-precision | 16 | 1 | 5 | 10 | 2 |
| Single-precision | 32 | 1 | 8 | 23 | 2 |
| Double-precision | 64 | 1 | 11 | 52 | 2 |
With this approach, the number of bits for the fraction has been reduced (i.e. for the 16-bits number it was reduced from 16 bits to 10 bits). It means that the fraction might take a narrower range of values now (losing some precision). However, since we also have an exponent part, it will actually increase the ultimate number range and also allow us to describe the numbers between 0 and 1 (if the exponent is negative).
For example, a signed 32-bit integer variable has a maximum value of 2³¹ − 1 = 2,147,483,647, whereas an IEEE 754 32-bit base-2 floating-point variable has a maximum value of ≈ 3.4028235 × 10³⁸.
To make it possible to have a negative exponent, the IEEE 754 standard uses the biased exponent. The idea is simple – subtract the bias from the exponent value to make it negative. For example, if the exponent has 5 bits, it might take the values from the range of [0, 31] (all values are positive here). But if we subtract the value of 15 from it, the range will be [-15, 16]. The number 15 is called bias, and it is being calculated by the following formula:
exponent_bias = 2 ^ (k−1) − 1
k - number of exponent bits
I’ve tried to describe the logic behind the converting of floating-point numbers from a binary format back to the decimal format on the image below. Hopefully, it will give you a better understanding of how the IEEE 754 standard works. The 16-bits number is being used here for simplicity, but the same approach works for 32-bits and 64-bits numbers as well.

Here is the number ranges that different floating-point formats support:
| Floating-point format | Exp min | Exp max | Range | Min positive |
|---|---|---|---|---|
| Half-precision | −14 | +15 | ±65,504 | 6.10 × 10⁻⁵ |
| Single-precision | −126 | +127 | ±3.4028235 × 10³⁸ | 1.18 × 10⁻³⁸ |
Be aware that this is by no means a complete and sufficient overview of the IEEE 754 standard. It is rather a simplified and basic overview. Several corner cases were omitted in the examples above for simplicity of presentation (i.e. -0, -∞, +∞ and NaN (not a number) values)
Code examples
In the javascript-algorithms repository, I’ve added a source code of binary-to-decimal converters that were used in the interactive example above.
Below you may find an example of how to get the binary representation of the floating-point numbers in JavaScript. JavaScript is a pretty high-level language, and the example might be too verbose and not as straightforward as in lower-level languages, but still it is something you may experiment with directly in the browser:
See the Pen bitsToFloat.js by mzekiosmancik (@mzekiosmancik) on CodePen.
References
You might also want to check out the following resources to get a deeper understanding of the binary representation of floating-point numbers:

